Temperature is important
There is an optimal temperature for a dough that just finished mixing and kneading. This has to do with the premise that you are now going to bulk ferment the dough and depending on the dough's contents, fermentation gets the best results (from a flavor perspective, which depends on speed, flour and mixing) when it starts at a certain temperature. If your source specifies this temperature (example is the CIA's Baking and Pastry book), you use it. Otherwise 78F, or 79F is a good guess.
The temperature of a mixed dough depends on the temperature of the main ingredients, being the flour, water (or milk etc.), and any preferments.
Contributions to final dough temperature
The following portion of the "Recipe" worksheet will aid in explaining what is going on:
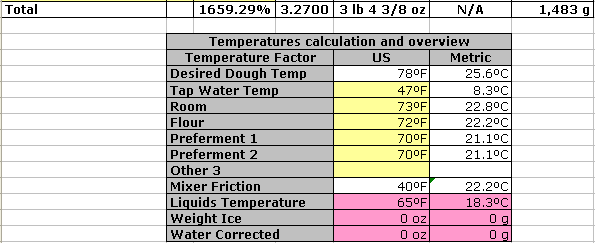
In this example, the main temperature contributors to the final dough are (a probe thermometer is your friend for all this):
- Ambient (room/kitchen) temperature. This temperature is relevant because with everything left to itself, the final temperature would settle here.
- Flour temperature. If this is significantly different from the room temperature, it will affect the temperature of the overall outcome. Flour typically contributes more than 50% of the final dough weight, so this is significant.
- Temperature of the (two) preferments used. The reasoning here is the same as for flour. The preferment may have been stored differently from the flour, so it may have a different temperature and is handled separately. The table has room ("Other 1", and "Other 2") for additional preferments, or other large contributing ingredients. Use as necessary.
- Temperature of the water/liquids used. The temperature of the water (milk, or other liquids) used is entered in this table. The desired dough temperature was entered at the top of the worksheet. The line for "Liquids Temperature" you see here, is what it should be to arrive at the desired final dough temperature. If your water source delivers water colder than this, use a microwave (and a probe thermometer) to warm it up. If your water source is warmer, the table will compute (on the "Weight Ice" line) the weight of ice cubes you would need to combine with some water ("Water Corrected") and mix into the dough, in order to arrive at the desired dough temperature. This only works if the liquid is water. Using ice cubes with milk will cool, but will also dilute the milk and will throw off (by a small amount) the hydration calculation.
- Mixer friction factor (not shown here, but entered in top left of worksheet). You will have to determine this for your specific setup emperically. You do that by mixing a dough as you normally would, and writing down all temperatures involved and measuring the ending temperature. You then calculate backwards to arrive at the mixer friction factor for this dough, this quantity and this specific mixing time.
Thus, in the example (which assumes 47F water source), we see that we need to warm up the water a bit, and no ice is needed. You will find that the "Water Corrected" is identical to what the basic formula lists.
TIP: As an alternative, and if you do not want to bother with precise ice measurements and crushing ice, just add some ice cubes to the water to cool it below the desired temperature. Use the microwave to correct it back up to what you need. This obviously only works if the water temperature you are looking for is above the freezing point.
How the calculation is done
The calculation is not correct from a physics perspective, but is a reasonable approximation, again under the assumptions that the ingredients listed have a roughly equal contribution. The basic formula (for degrees Fahrenheit) is to multiply the desired dough temperature by the number of temperature contributors involved (4 in this example: room, flour, preferment, mixer) and subtract each contributor's temperature.
This approximation has been used for a long time, and succesfully at that, so why is this? Remember that you have to emperically determined your mixer friction factor for each specific dough and setup? Differences from the above calculation are caused by:
- Not all ingredients have equal weights and thus do not contribute equally to temperature changes
- Not all ingredients conduct heat the same
- Other chemical reactions may occur, causing heat to be added or taken away
The differences from the above calculation are all absorbed into the friction factor that you come up with. Thus its name is a little misleading in that it not only accounts for mixer friction (which is often the majority of it), but also for all these other changes.
Note that while for all contributors except mixer friction, we input an actual temperature, and conversions from Fahrenheit to Celcius are provided (and show the expected values). Mixer friction, however, is a temperature difference and hence conversion to the equivalent amount in Celcius is not the same. A normal conversion from F to C involves subtracting 32 (freezing temperature) and multiplying by 5, dividing by 9. For a temperature difference conversion, you leave out the subtraction of 32 (because it cancels out). Thus a mixer friction factor of 40F is equivalent to 22.2C, and not to 4.4C!
If the calculated water temperature would come out to be below freezing, we have a problem. We can't get ice out of the tap, let alone ice of a specific temperature. Converting ice into liquid water takes substantial energy. If we add ice to the dough mix and it converts back to water, it needs this energy, which is extracted from the rest of the ingredients, cooling the dough.
The amount of ice needed (in pounds) is computed by multiplying the total weight of all liquid ingredients, expressed in pounds, by the difference in temperature between the source water and the desired water temperature and then divide by the sum of source water temperature and 112. This is the formula for Fahrenheit. If you are working in Celcius, express the weight in kilograms, and instead of 112 use 80 (the original 112 + 32 from the conversion from F to C, multiplied by 5/9). This will give the amount of ice in kilograms.
The ice should be flaked or crushed ice in order to increase the contact surface and to facilitate the liberation of the latent heat.
Here is a copy of an article from Baker's Exchange that goes into more detail and examples.